Aufgabe 10, Antwort A:
Wenn der systolische Blutdruck einer Bevölkerung mit einem Erwartungswert von µ = 125 mmHg und einer Standardabweichung von σ = 10 mmHg normalverteilt sei, ist dann die Wahrscheinlichkeit, dass eine zufällig daraus ausgewählte Person einen Blutdruck höher als 120 mmHg hat, ungefähr
0,31?
Sie sind auf dem richtigen Weg, aber
Sie haben die Wahrscheinlichkeit der Personen berechnet, die einen Blutdruck kleiner oder gleich 120 mmHg haben.
Da die Daten normalverteilt sind, können wir sie einfach in die Standardnormalverteilung mit der Formel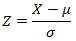 
transformieren. − Das haben Sie richtig erkannt.
Beim Auslesen in der Tabelle muss man nun aber beachten, dass aufgrund der Symmetrie der Glockenkurve Φ(-z) = P(Z ≤ -z) = P(Z ≥ z) = 1 - Φ(z) gilt. Außerdem wollen wir die Wahrscheinlichkeit dafür bestimmen, dass der Blutdruck größer als 120 ist, sodass der gesuchte Wert nur die Gegenwahrscheinlichkeit angibt. − Dieser Schritt fehlt Ihnen noch.
Wissen Sie nun, welche Antwort die richtige Lösung ist?
