Aufgabe 10, Antwort D:
Wenn der systolische Blutdruck einer Bevölkerung mit einem Erwartungswert von µ = 125 mmHg und einer Standardabweichung von σ = 10 mmHg normalverteilt sei, ist dann die Wahrscheinlichkeit, dass eine zufällig daraus ausgewählte Person einen Blutdruck höher als 120 mmHg hat, ungefähr
0,69?
Richtig!!! − Bei dieser Aufgabe muss man zweimal um die Ecke denken, aber das haben Sie mit Bravur gemeistert.
Gesucht ist P(X>120). Um dies zu bestimmen, transformiert man die Zufallsvariable mit der Formel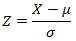 
in die Standardnormalverteilung.
Man erhält Z=-0,5. Für negative Werte gilt (-z): Φ(-z) = P(Z ≤ -z) = P(Z ≥ z) = 1 - Φ(z) aufgrund der Symmetrie der Glockenkurve. Daher rechnet man Z = 1 - 0,5 = 0,5 und mit Hilfe der Tabelle kommt man auf eine Wahrscheinlichkeit von 0,6915 ≈ 0,69.
Sie haben diese Aufgabe "Sherlock Homes"-würdig gelöst. Machen Sie weiter so ...
