Der zentrale Grenzwertsatz besagt, dass - unter sehr allgemeinen Bedingungen - die Summe einer großen Anzahl von Zufallsvariablen normalverteilt ist. Mathematisch präzise formuliert lautet dieser Satz:

Seien X_i (i = 1, 2, …, n) unabhängige, identisch verteilte Zufallsvariablen mit dem Erwartungswert µ und der Varianz σ2. Dann ist die Summe der X_i asymptotisch normalverteilt mit dem Erwartungswert n ⋅ µ und der Varianz n ⋅ σ2.

Also ist die Variable:

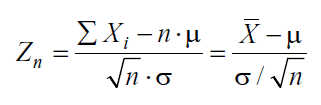
asymptotisch standardnormalverteilt.
Daraus ergeben sich unmittelbar einige wichtige Konsequenzen bezüglich der